Last week we made MAX 24.2 available for download, and we shared more details in the MAX 24.2 announcement and the Mojo open-source blog posts. In this blog post. I’ll dive a little deeper into all the new features specifically in Mojo🔥. This will be your example-driven guide to Mojo SDK 24.2, as part of the latest MAX release. If I had to pick a name for this release, I’d call it MAXimum⚡ Mojo🔥 Momentum 🚀 because there is so much much good stuff in this release, particularly for Python developers, adopting Mojo. 

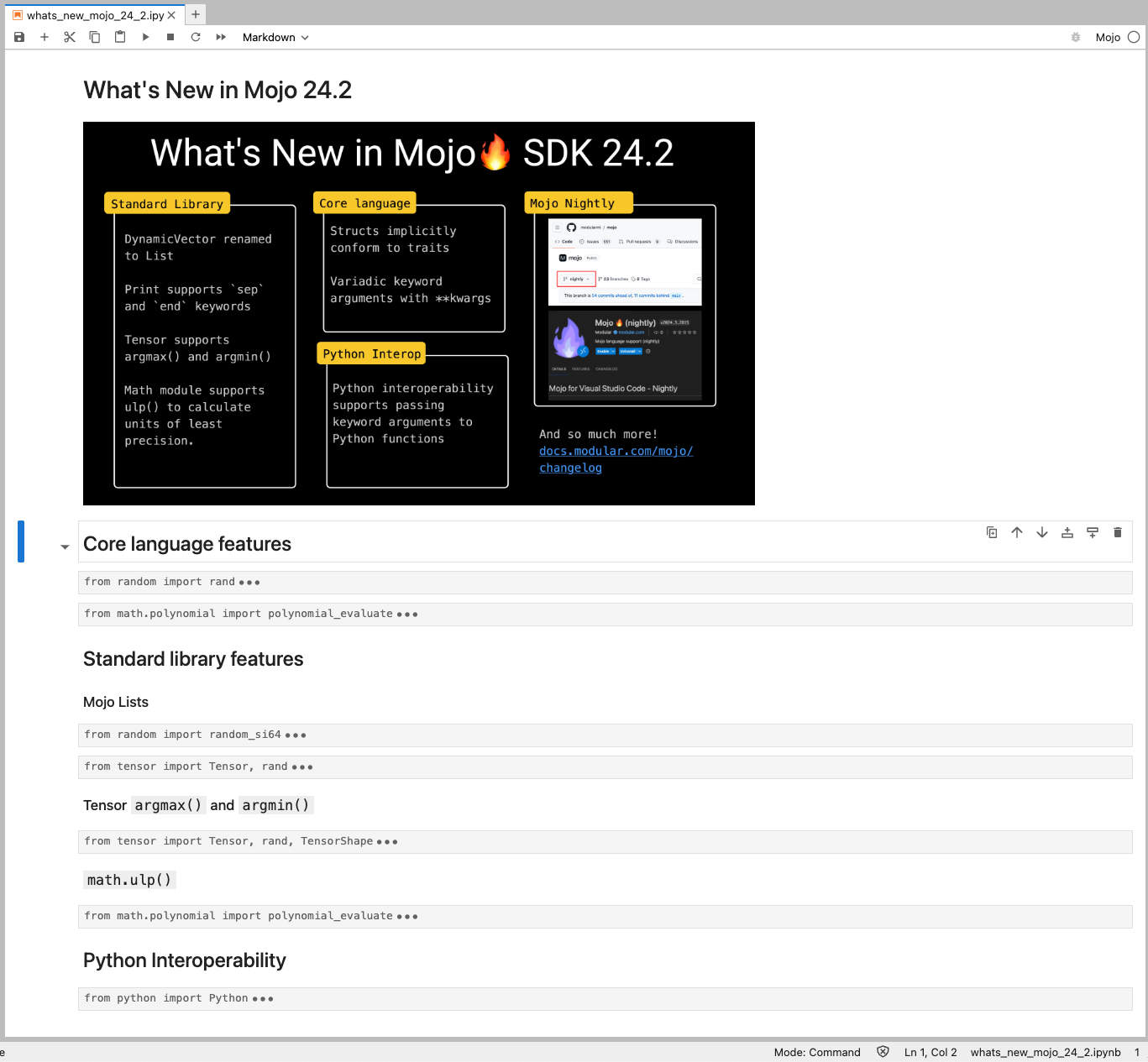
Here’s a summary of all the key features in this release.

Through the rest of the blog post, I’ll share each feature listed above with code examples that you can copy/paste and follow along. You can also access all the code samples in this blog post in a Jupyter Notebook on GitHub. As always, the official changelog has an exhaustive list of new features, what’s changed, what’s removed, and what’s fixed. And before we continue Don’t forget to upgrade your Mojo🔥. If you haven’t already, head over to the getting started page and follow the 3 simple steps to update Mojo to the latest release. Let’s dive into the new features.

New Mojo standard library features

Starting with this release, Mojo standard library is now open-source! You can head over to Mojo repository on GitHub where you’ll find the source code and contributing guide. Here are the new features in the Mojo standard library, explained with code examples.

DynamicVector is now called List

I had previously ignored using DynamicVector because I didn’t realize it’s similar to Python’s list data container. Starting with this release, DynamicVector has been renamed to List. If you are a Python list user, then you should feel right at home with Mojo List. Let’s take a look at a simple stack-based sorting algorithm using Lists in Mojo.

Output:

In the above example, you can see that working with Mojo Lists are easy and very similar to Python Lists. The List functions I use are:

1. Initializations: List[Int]() and List[Int](list). The former creates an empty List and the latter creates a deep-copy of an existing list 
2. Append and pop_back: append function introduces a new value to the List, and pop_back removes the last element from the list.

See the List doc page for all the supported List methods. Lists are not confined to Int types, they can hold any Mojo type that implements the CollectionElement trait. Here is an example of a list holding Tensors of different sizes.

Output:

Print supports sep and end keywords

Lists don’t support print() today, and I will use this as an opportunity to show you the new print() features. In the print_list() function above you can see that we use Python style sep and end keywords. The sep keyword argument specifies the string that should be used to separate the items that are passed to the print() function. The end keyword argument specifies the string that should be printed at the end of the print() function call. Using both, I wrote the list printing function in the previous example.

The output of calling our custom print_list():

New ulp() function in math module

Moving on, there is a new addition to the math module in the standard library - the ulp() function. The ulp() function is also called Units of Least Precision, and it returns the distance between the floating-point number x and the next representable floating-point number in magnitude. This is useful to define a tolerance for comparing floating-point numbers, and to understand the precision of a floating-point number at a particular value. Let’s take a look at an example that uses ulp(). 

The Newton-Raphson method is a way to find a good approximation for the root of a function, i.e. the value of the variable that makes the function value zero. It’s an iterative algorithm that iterates on x using the following formula, until convergence is reached.

$$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$$

We can break from the iterations if changes in x falls below some threshold which we define using math.ulp(). Consider this polynomial:

$$f(x) = x^3 - 2x^2 + 3x - 6$$

Now plug in the value $x=2$ and $f(x)$ become zero. The polynomial of degree 3 must have 2 other roots, and in this case they are imaginary, so we’ll ignore them for now. Here's Newton-Raphson's method of finding the root.

In the above code we provide both an early stop tolerance value, and take the maximum of tolerance and (tolerance, ulp(x_new)) to decide if we should terminate our iterative algorithm.

If you run the code you’ll see that the algorithm finds the root of the polynomial and terminates after 15 steps.

If I want it to converge sooner, I can increase the manual tolerance to say 1e-2 and it converges in 13 steps with an approximate solutions

Output:

math.ulp is useful to compare floating point numbers, and are especially useful in iterative algorithms used in machine learning and numerical optimization problems.

New Mojo <-> Python interoperability features

One of the highlights of this release for me is the ability to pass keyword arguments to Python functions. For example, in earlier versions if you wanted to use MatplotLib to create a figure you’d have to do it this way:

Now, with keyword arguments you can:

This makes using Python modules much easier. Building on our previous example of finding the root of the polynomial $f(x) = x^3 - 2x^2 + 3x - 6$, let’s visualize it using MatplotLib to see where the graph cross line y=0 and you can see that it crosses at x=2 which agrees with the value we estimated using Newton-Raphson’s method.

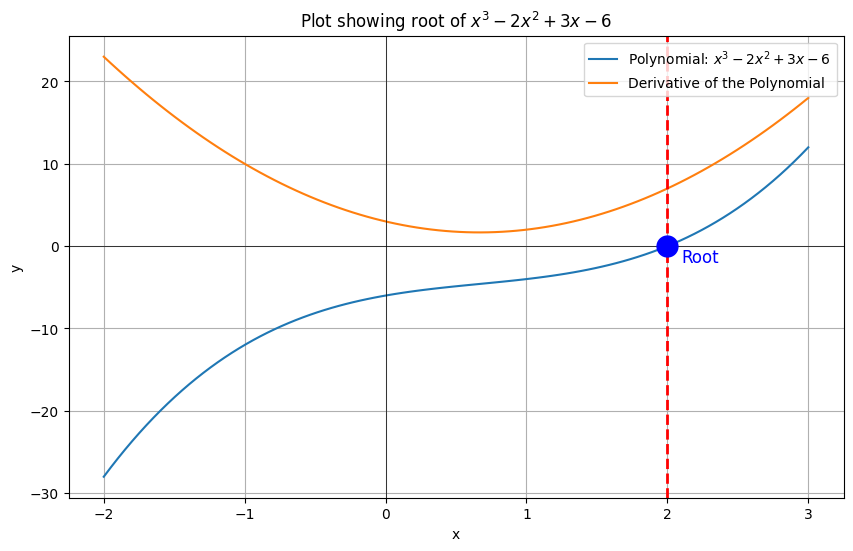
Here’s the Mojo code with Python interoperability and the new Python keyword arguments feature, that you can use to generate the graph.

New core language features

Mojo 24.2 also includes new core language features that makes it easier to write structs and to work with keyword arguments to functions.

Structs implicitly conform to traits

This is my favorite new core language feature, because I no longer have to specify all the traits in the Struct’s definition. For example, previous we had to define a Struct like this:

With this new feature, you can skip mentioning the traits, as long as you’ve implemented the methods in the Struct. Here is a working example:

Output

However, as the changelog notes, we still strongly encourage you to explicitly list the traits a struct conforms to when possible.

Python style variadic keyword arguments: **kwargs

Mojo now has support for variadic keyword arguments: **kwargs to support an arbitrary number of keyword arguments. For example, here is a function that evaluates polynomials of user specified degree via coefficients provided as keyword arguments.

Let’s evaluate a degree 3 polynomial function at x=42 and compare its results with the standard library’s polynomial_evaluate() function.

Output:

Using keyword arguments, we can increase the degree of the polynomial by providing additional coefficients and compare the results:

Output

New Mojo nightly build, nightly Visual Studio Code extension and open-source standard library

With the release of the open-source Mojo standard library, the Mojo public repo now has a new branch called Nightly, which is in sync with the Mojo nightly build. All pull requests should be submitted against the nightly branch, which represents the most recent nightly build. 

The nightly build also has an accompanying nightly Visual Studio Code extension. Note that you can only use one Mojo extension at a time. If you’re using the nightly extension, please disable the release extension.

Read more about contributing to open-source in our contributing guide on GitHub.

But wait, there is more!

We’re excited for you to try out the latest release of Mojo. For a detailed list of what’s new, changed, moved, renamed, and fixed, check out the changelog in the documentation. 

All the examples I used in this blog post are available in a Jupyter Notebook on GitHub, check it out!

Additional resources to get started:

• Download MAX and Mojo
• Head over to the docs to read the Mojo🔥 manual and learn about APIs
• Explore the examples on GitHub
• Join our Discord community
• Contribute to  discussions on the Mojo GitHub
• Read and subscribe to Modverse Newsletter 
• Read Mojo blog posts, watch developer videos and past live streams
• Report feedback, including issues on our GitHub tracker

Until next time! 🔥