On Valentine’s Day yesterday, I wanted to create something special to celebrate my love for Mojo and Python. My search on the interwebs led me to a nifty little equation that plots a heart. The equation is quite simple and I’ll refer to this as the “heart equation” through the rest of this blog post:

$f(x) = (x)^{\frac{2}{3}} - 0.9 \sqrt{3.3 - x^2} \sin(a \pi x)$

In this equation if you vary the variable a from 0 to 20 in small increments, you get this cool animation:

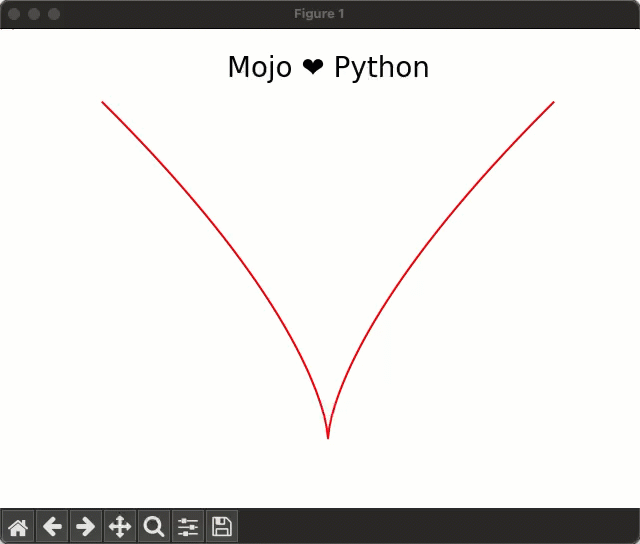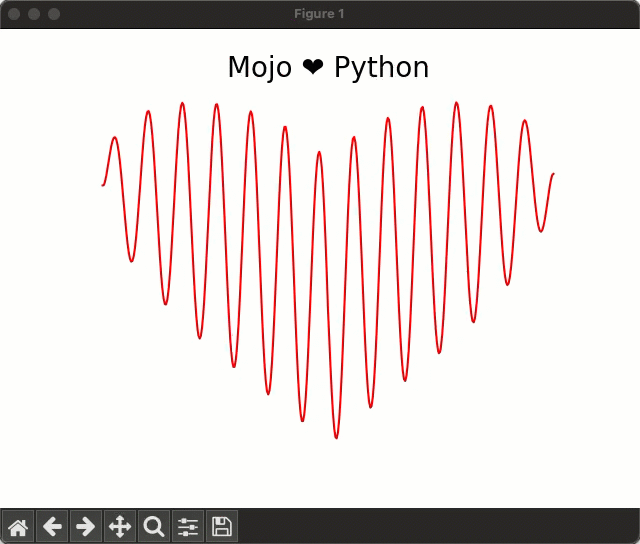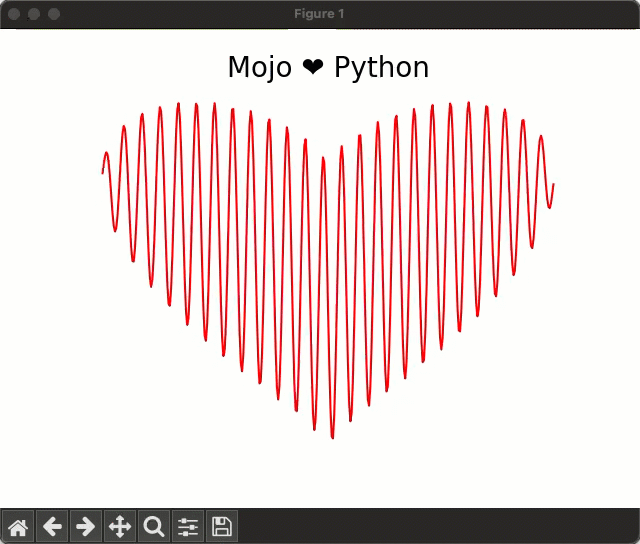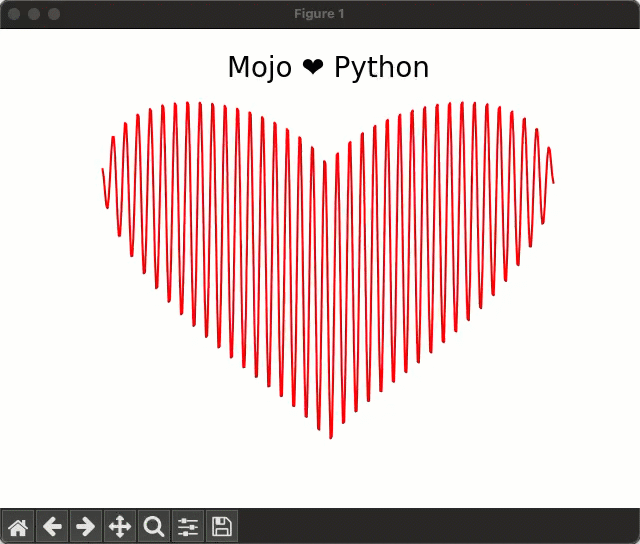
The heart equation is fairly easy to implement in Python using NumPy, but in this blog post I'll show you how you can implement it in Mojo🔥. Mojo is still young and its standard library doesn’t yet have a robust NumPy-like data structure for implementing math equations, but with relatively low effort you can implement a custom data structure (I’ll call MojoArray in this blog post) that supports basic vectorized math operations we need, to implement the heart equation. Once we've created our MojoArray data structure, we can implement the equation and plot it using the following code:

Since Mojo offers first-class support for Python interoperability, we’ll see how you can do all the computation in Mojo🔥 and leverage Python and Matplotlib library to plot the animation you see above.

Note: The code for this example is available on GitHub. In this blog post, I’ll only share specific code snippets to explain key implementation details.

What you’ll learn:

1. How to create a custom Mojo🔥 data structure that lets do vectorized math operations
2. How to use double underscore aka dunder methods to overload math operators that make writing math equations easy
3. How to use Mojo standard library Math functions that operate on SIMD type and extend them to work on your data structure
4. How to leverage Python libraries to import NumPy arrays and plot using Matplotlib

Creating an Array data structure that supports vectorized Math operations

To implement the heart equation, I need a data structure that supports vectorized Math operations. For example, in this equation x is a vector, and I need sqrt, pow, sin, add, mul and div to operate on vectors.

$f(x) = (x)^{\frac{2}{3}} - 0.9 \sqrt{3.3 - x^2} \sin(a \pi x)$

Mojo Math module in the standard library supports common mathematical operations but they operate on SIMD types only. SIMD types allow you perform a single operation on small vectors who’s length depends on the CPU type. For example, to compute sin on a SIMD vector, in Mojo you can run:

Output:

Which gives you very small numbers as you’d expect, since sin of approximate value of pi, is approximately 0. To implement the heart equation, we'll need to work with large vectors, therefore, we need a Mojo struct that offers methods to perform Math operations on large vectors, not just SIMD types.

Mojo standard library offers a Tensor data structure that can store higher order tensors, but it is quite an overkill for this simple example. The Tensor type also doesn’t support basic Math operations which we need. With a simple, custom data structure called MojoArray, we can only implement the features we need.

Here is the skeleton of the MojoArray data structure that we’ll be using to calculate our heart equation. 

The MojoArray data structure is parameterized on dtype which defaults to float64, which is also the default type of NumPy arrays. MojoArray struct also defines double underscore aka dunder methods that overload common mathematical operations such as addition, subtraction, multiplication to work on two MojoArrays or MojoArray and scalar values.

Let’s take a closer look at the implementation details of a few of these. Most of the math operations fall into one of these categories:

Elementwise transforms: _elemwise_transform[]()

This helper function implements Trigonometric functions, and abs. that transform a MojoArray. _elemwise_transform[]() applies the function func on all the elements in the MojoArray.

I use _elemwise_transform to implement sqrt, cos, sin and abs:

Elementwise vector-scalar operations _elemwise_scalar_math[](): 

This helper function implements multiplication, addition, and subtraction between MojoArrays and scalars. _elemwise_array_math accepts a scalar and applies the function func on all the elements in the MojoArray.

We use _elemwise_scalar_math to implement negative, addition, subtraction, and multiplication between a vectors and a scalar:

Elementwise vector-vector operations _elemwise_array_math[]()

This helper function implements multiplication, addition, and subtraction between two MojoArrays. 

We use _elemwise_array_math to implement addition, subtraction, and multiplication between two vectors

Implementing the Heart Equation

With our MojoArray data structure in place, we’re now ready to implement our heart equation. In the main() function, we perform the following steps:

1. Load Python modules NumPy and Matplotlib
2. Create NumPy arrays and use that to instantiate our MojoArray data structure
3. Implement the heart equation y = (x**2)**(1/3.) - 0.9*((3.3-(x*x)).sqrt())*(a[i]*3.14*x).sin()
4. Loop over values of a to create the animation I showed at the top of the blog post.

Conclusion

Happy Valentines’ week! Hope you enjoyed reading this blog post on how to implement the heart equation in Mojo. My hope is that you can reuse parts of this example in your own workflows. Download Mojo to run this example and share your feedback with us! Here are some additional resources to get started:

• Get started with downloading Mojo
• Head over to the docs to read the programming manual and learn about APIs
• Explore the examples on GitHub
• Join our Discord community
• Contribute to  discussions on the Mojo GitHub
• Read and subscribe to Modverse Newsletter 
• Read Mojo blog posts, watch developer videos and past live streams
• Report feedback, including issues on our GitHub tracker

Until next time🔥!